티스토리 뷰
문제
https://oj.uz/problem/view/JOI19_naan
문제 보기 - Naan (JOI19_naan) :: oj.uz
문제 보기 - Naan (JOI19_naan)
oj.uz
길이 L의 빵이 주어진다. 각 빵은 길이 1 단위로 서로 다른 맛의 소스가 칠해져 있다. 이때 N명의 사람들의 단위 길이의 소스별 행복도가 주어진다. 빵을 정확히 N개의 조각들로 나누어, 각 사람에게 하나씩 조각을 나누어 줄 때, 다음 조건을 만족해야 한다.
(전체 빵을 모두 먹었을 때의 행복도)/N <= (그 조각만 먹었을 때의 행복도)
모든 사람이 위 조건을 만족할 수 있도록 빵을 N개의 조각으로 나누고, 조각을 각 사람에게 배정해야 한다.
\(N<=2000\)
\(L<=2000\)
풀이
가장 먼저, 만약 조각별 그 조각을 가져가는 사람의 순서가 정해져 있고, 조각을 어떻게 나눠야 할지 생각해보자.
첫 번째 사람별로 자신이 지금부터 먹을 수 있는 위치부터 먹기 시작하여 조건을 만족하는 그 순간까지만 먹으면 된다. 이와 같이 조건의 수치를 넘는 최소의 위치까지만 잘라 먹고 다음 사람에게 넘겨주는 과정을 반복하면 가능 / 불가능 여부를 따질 수 있다.
사람의 순서가 정해져 있지 않다면 어떻게 해결해야 할까?
우선, 각 사람별 행복도의 하한이 (전체 빵을 모두 먹었을 때의 행복도)/N 이므로 앞에서부터 최대한 그리디하게 쪼개면 각 사람별로 전체 빵을 정확히 N개의 조각으로 쪼개어질 것이다.
이 조각들만을 이용하여 문제를 해결할 수는 없을까?
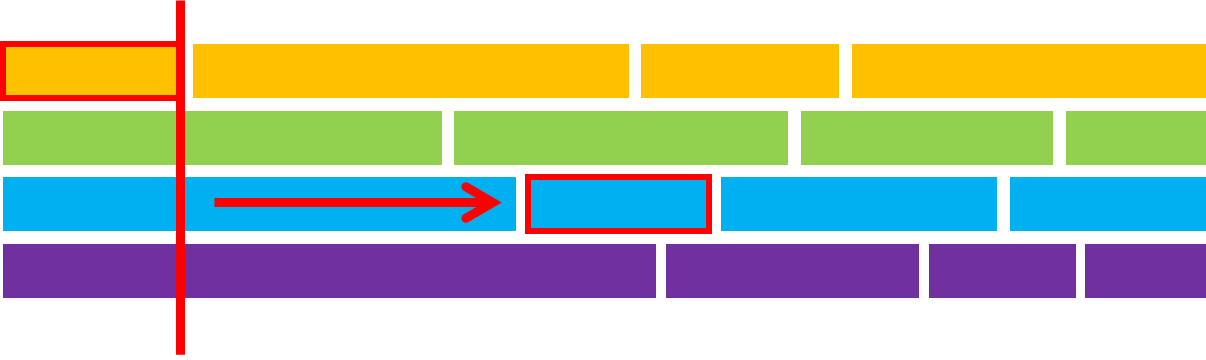
Observation 1 : 위 과정을 통해 얻은 조각들 중, $i$번째 단계에서는 아직 선택되지 않은 사람들 중 $i$번째의 끝나는 위치가 가장 작은 조각을 그리디하게 선택해 주면 무조건 답을 얻을 수 있다.
귀납법을 이용하여 증명할 수 있다.
먼저 지금 아직 선택하지 않은 사람들 중 $i$번째 조각들을 끝나는 위치를 기준으로 정렬하고 생각하자. 그 중 가장 앞쪽의 (끝나는 위치가 가장 작은) 조각을 선택한다면, 그 다음 단계에서도 남은 조각들 중 끝나는 위치가 가장 작은 조각을 선택할 수 있음을 보이면 된다. 끝나는 위치가 가장 작은 조각을 제거하였으므로, 남은 사람들의 $i+1$번째 조각들의 시작점은 모두 방금 제거한 조각의 끝나는 위치보다 크거나 같기 때문에 다음에 선택한 조각과 방금 제거한 조각은 무조건 겹치지 않고, 조건을 만족하며 선택할 수 있다.
따라서 위 과정을 반복하여 선택해주면 되고, $O(N^2)$의 시간에 가장 작은 조각을 그냥 계산해 주면 된다.
유리수 표현에서의 대소관계에서 int128이 필요함에 주의하자.
시간 복잡도 : $O(NL+N^2)$
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
const int MAXN = 2000;
int N, L;
ll A[MAXN+10][MAXN+10];
struct Frac
{
ll x, y;
Frac() {}
Frac(ll _x, ll _y)
{
x=_x; y=_y;
norm();
}
void norm()
{
ll g=__gcd(x, y);
x/=g; y/=g;
}
};
bool operator >= (Frac p, Frac q) { p.norm(); q.norm(); return (__int128)p.y*q.x>=(__int128)q.y*p.x; }
Frac B[MAXN+10][MAXN+10];
bool vis[MAXN+10];
int ans[MAXN+10];
int main()
{
scanf("%d%d", &N, &L);
for(int i=1; i<=N; i++)
{
for(int j=1; j<=L; j++) scanf("%lld", &A[i][j]), A[i][j]+=A[i][j-1];
for(int j=1, p=1; j<=N; j++)
{
for(; p<L && A[i][p]*N<=j*A[i][L]; p++);
ll t=j*A[i][L]-N*A[i][p-1];
B[i][j]=Frac(N*(A[i][p]-A[i][p-1]), (p-1)*N*(A[i][p]-A[i][p-1])+t);
B[i][j].norm();
}
}
for(int i=1; i<=N; i++)
{
Frac t; int val=-1;
for(int j=1; j<=N; j++)
{
if(vis[j]) continue;
if(val==-1 || t>=B[j][i]) val=j, t=B[j][i];
}
if(i<N) printf("%lld %lld\n", t.y, t.x);
ans[i]=val;
vis[val]=true;
}
for(int i=1; i<=N; i++) printf("%d ", ans[i]); printf("\n");
}'JOISC > 2019' 카테고리의 다른 글
| JOISC19 Dishes (0) | 2020.09.10 |
|---|---|
| JOISC19 Antennas (0) | 2020.09.08 |
| JOISC19 Examination (0) | 2020.09.07 |
- Total
- Today
- Yesterday
- Segment Tree
- offline
- APIO
- CHT
- convex hull
- Fenwick Tree
- DFS
- ⭐
- Union Find
- Codeforces
- ioi
- Shortest path
- Floyd-Warshall
- Parametric Search
- tree
- graph
- Sqrt Decomposition
- HLD
- Merge Sort
- Centroid Decomposition
- BOJ
- Sparse Table
- Greedy
- stack
- Line sweeping
- Persistent Segment Tree
- DP
- Divide & Conquer
- Interactive
- Lazy Propagation
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
