JOISC17 Sparklers

JOISC/2017

JOISC17 Sparklers

arnold518 2020. 11. 9. 23:29

문제

문제 보기 - Sparklers (JOI17_sparklers) :: oj.uz

문제 보기 - Sparklers (JOI17_sparklers)

oj.uz

수직선 위에 N명의 사람들이 폭죽을 하나씩 들고 서 있다. 처음에는 K번째 사람의 폭죽에만 불이 붙어 있으며, 폭죽에 불이 처음 붙은 후로부터 T초 동안만 불꽃이 유지된다. 불꽃이 꺼지기 전에 어떤 다른 사람과 같은 위치에 있게 되면 그 사람에게 불꽃을 옮길 수 있다. 또한, 각 사람이 1초동안 움직일 수 있는 최대 거리인 속도 X가 정해져 있을 때, 모든 사람의 폭죽에 불이 한번씩 붙을 수 있기 위한 최소의 정수 속도 X를 구해야 한다.

$N<=100000$

풀이

Observation 1 : 모든 사람이 정지하지 않는 최적해가 존재한다.

최적해에서 정지하는 사람이 있다고 생각하자. 정지해 있는 것과 같은 효과로 정지해 있을 시간만큼 왼쪽으로 이동했다가 다시 오른쪽으로 이동하면 절대 정지하지 않을 수 있다.

Observation 2 : 불이 한번이라도 켜진 사람들은 K번째에서부터 시작해서 왼쪽, 오른쪽으로 구간 형태로 퍼져나간다.

불꽃이 퍼져 나가기 시작하는 점이 중간의 한 점이고, 계속해서 오른쪽 혹은 왼쪽 사람에게 전파하기 때문에 전체 켜진 사람들은 구간을 이룬다. 또한, 현재 불꽃을 소지하고 있지 않은 점들은 무조건 불꽃을 소지하고 있는 점들 방향으로 움직이는 것이 최적이다.

위 두 관찰로, 모든 사람들이 멈추지 않고 움직이며, 불꽃은 가운데 에서부터 퍼져 나가는 형태임을 알 수 있다. 또한, 불꽃을 갖고 있는 구간 밖의 사람들은 계속해서 가운데 구간을 향하여 들어오는 형태이다.

Observation 3 : 어떤 순간에라도 동시에 불이 켜져 있는 사람들은 존재하지 않는다.

만약 어떤 순간에, 한 사람의 불이 아직 꺼지지 않은 상태에서 다음 사람의 불을 붙였다고 생각하자. 만약, 불을 붙인 직후 서로 다른 방향으로 움직이지 않는다면, 즉 분리하지 않는다면, 분리하는 순간까지 기다렸다가 최대한 늦게 불을 붙이는 것이 이득이라는 것을 알 수 있다. 따라서 사람 A의 불이 꺼지기 전에, B가 불을 붙였고, 불을 붙힌 직후 A와 B는 반대 방향으로 움직이는 상황이라는 것을 알 수 있다. 일반성을 잃지 않고 A는 왼쪽으로, B는 오른쪽으로 움직였다 가정한다. B는 A와 분리한 직후 오른쪽으로 움직이다, 오른쪽에서 어떤 새로운 사람 C와 만나게 된다. 이때 이 사람은 아직 불이 붙지 않은 사람이며, 왼쪽으로만 이동하고 있다. 이제, 상황을 조금 변형해서, B가 A와 분리한 순간이 조금 더 늦어서 A와 함께 조금 더 왼쪽으로 간 후, 그 다음 분리하여 다시 C와 만난다고 생각하자. 이 두 상황에서 변함없이 A와 C는 왼쪽으로 일정하게 이동하고 있기 때문에 B, C가 교차한 이후 C의 오른쪽에 있는 사람들과 C의 상대적 관계는 변하지 않는다. 즉, 이 또한 최적해라는 의미이다.

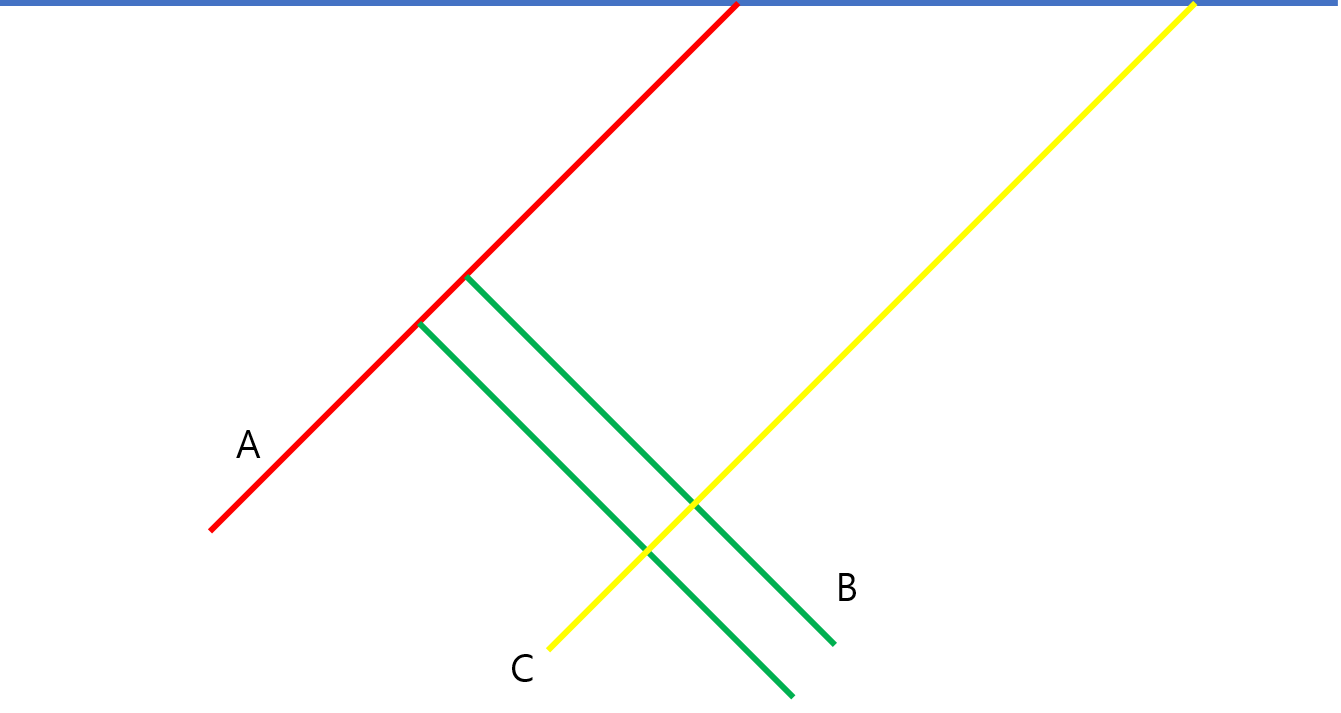
위 증명으로 얻을 수 있는 것은 A와 함께 최대한 움직이다, A가 꺼지기 직전에 B가 불을 옮겨도 문제가 없다는 뜻이다. 즉, 어떠한 두 사람이 동시에 불을 키고 있는 상황은 존재하지 않는다.

Observation 4 : 최적해는 K번째 사람이 이동하며 주변의 사람들과 순차적으로 한 명씩 만나가며, 만나는 사람들은 만난 이후 계속 K번째 사람을 따라 다니며 불이 꺼지기 직전 불을 옮긴다.

위 관찰을 종합적으로 정리하면 불을 계속 연속적으로 전달해 나가는 과정이고, 중심에서 주변의 사람들로 한 명씩 불을 옮긴다. 이 때 아직 불을 붙이지 못한 사람은 계속하여 중심의 불을 갖고 있는 사람을 향해 달려온다.

이 때 우리는 K번째 사람이 그 다음에 어느 방향으로 이동할지만 정해주며, 최종 교차점까지 불이 꺼지지 않을 수 있는가만 확인해주면 된다.

Subtask 2

위 관찰을 통해 K번째 사람이 그 다음으로 어느 방향으로 갈지 정해주는 과정을 DP를 통해 해줄 수 있다.

전체적인 풀이의 방향은 속도에 대한 파라마트릭 서치를 통해 속도를 정해준 후, 각 속도마다 가능/불가능 여부를 따져 주는 것이다.

또한, 구간 $[l, r]$만을 하나로 합칠 수 있는 필요충분조건을 확인해보자. 속도는 $X$이다.

위 직각이등변삼각형 그림에서 $[l, r]$을 합치는데 드는 시간은 $\frac{X_r-X_l}{2X}$이다. 이제, 이 시간까지 불이 꺼지지 지 않기 위해서는 $(r-l)T$의 시간보다 작거나 같어야 한다.

Observation 5 : $\frac{X_r-X_l}{2X}<=(r-l)T$가 성립해야 한다.

식을 정리하면 $X_r-2rTX<=X_l-2lTX$를 만족해야 한다.

따라서 $[K, K]$에서 $[1, N]$까지 조건을 만족하는 구간만 지나고 도달할 수 있는가를 확인하면 된다.

Subtask 3

$B_i=X_i-2iTX$라 정의할 때, $B_r<=B_l$를 만족하며 $[K, K]$에서 $[1, N]$으로 도달할 수 있는지 선형 시간복잡도에 확인하면 된다.

다음과 같은 그리디 알고리즘을 통해 해결한다.

$[1, K]$중 최댓값의 위치를 GL, $[K, N]$중 최솟값의 위치를 GR이라 하자.

Observation 6 : 전체 경로를 $[K, K]$ -> $[GL, GR]$ -> $[1, N]$으로 나눌 수 있다.

만약 $[GL, GR]$을 지나지 않는 유효한 경로가 존재한다 하자. 일반성을 잃지 않고 GL을 먼저 만난다고 하자. 오른쪽 포인터가 GR에 도달하기 전 GL에서 탈출하여 더 왼쪽의 점 P에서 GR에 도착하게 된다. GL에서 탈출한 순간부터 P에 도달하기까지의 모든 왼쪽 포인터 이동 동작들은 GR에 도착하고 난 이후에 해도 된다. GL이 최대, GR이 최소이므로, 다음과 같이 변형할 수 있으며, 이와 같이 변형하여도 손해가 되지 않는다.

$[K, K]$ -> $[GL, GR]$ -> $[1, N]$은 $[K, K]$ -> $[GL, GR]$, $[1, N]$ -> $[GL, GR]$로 분리하여, 똑같은 문제를 두번 푼다고 생각하자.

왼쪽 포인터를 움직이는 이동을 L 이동, 오른쪽 포인터를 움직이는 이동이는 이동을 R 이동이라 하면 최적해는 LLLRRRRLLLRRLLR과 같이 L과 R이 적절히 조합되어 구성된다. L에서 R로 바뀌는 전환점, R에서 L로 바뀌는 전환점마다 포인터의 위치에 주목하자.

Observation 7 : 최적해는 현재 이동시킬 수 있는 왼쪽 포인터 중 값이 최대인 지점으로 이동시킨 후, 다시 현재 이동시킬 수 있는 오른쪽 포인터 중 값이 최소인 지점으로 이동하는 과정을 꼴이다.

위 알고리즘을 통해 $[K, K]$ -> $[GL, GR]$, $[1, N]$ -> $[GL, GR]$가 도달 가능한 경로인지 확인한다. 이를 파라마트릭 서치와 함께 문제를 해결할 수 있다.

시간 복잡도 : $O(NlogX)$

#include <bits/stdc++.h>
using namespace std;
 
typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
 
const int MAXN = 100000;
const ll INF = 1e18;
 
int N, K;
ll T, A[MAXN+10], B[MAXN+10];
 
bool decide(ll X)
{
	X*=2;
	if(T*X>(ll)1e9) return true;
	for(int i=1; i<=N; i++) B[i]=A[i]-i*T*X;
 
	int gl=1, gr=N;
	for(int i=1; i<=K; i++) if(B[gl]<=B[i]) gl=i;
	for(int i=K; i<=N; i++) if(B[gr]>=B[i]) gr=i;
 
	int l=K, r=K;
	ll lv=B[l], rv=B[r];
	while(gl<=l || r<=gr)
	{
		int bl=l, br=r;
		for(; l>=gl && B[l]>=rv; l--) lv=max(lv, B[l]);
		for(; r<=gr && B[r]<=lv; r++) rv=min(rv, B[r]);
		if(l==bl && r==br) return false;
	}
 
	l=1, r=N;
	lv=B[l], rv=B[r];
	while(l<=gl || gr<=r)
	{
		int bl=l, br=r;
		for(; l<=gl && B[l]>=rv; l++) lv=max(lv, B[l]);
		for(; r>=gr && B[r]<=lv; r--) rv=min(rv, B[r]);
		if(l==bl && r==br) return false;
	}
	return true;
}
 
int main()
{
	scanf("%d%d%lld", &N, &K, &T);
	for(int i=1; i<=N; i++) scanf("%lld", &A[i]);
 
	ll lo=-1, hi=1e9+10;
	while(lo+1<hi)
	{
		ll mid=lo+hi>>1;
		if(decide(mid)) hi=mid;
		else lo=mid;
	}
	printf("%lld\n", hi);
}

저작자표시