Andrew's Chain

Andrew's Chain은 주어진 점 집합들의 Convex Hull을 $O(NlogN)$에 구할 수 있게 해주는 Graham's Scan과는 다른 알고리즘이다.

 

Graham's Scan과는 다르게 Upper Hull과 Lower Hull로 분리해낼 수 있다는 장점이 있고, 정렬 또한 각도 정렬이 아닌 단순한 x축 기준 정렬만 필요하다.

 

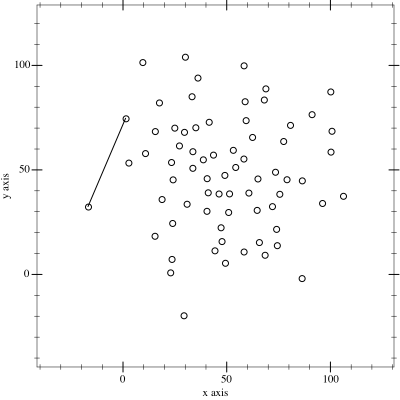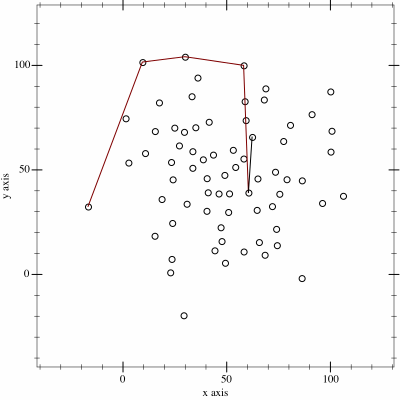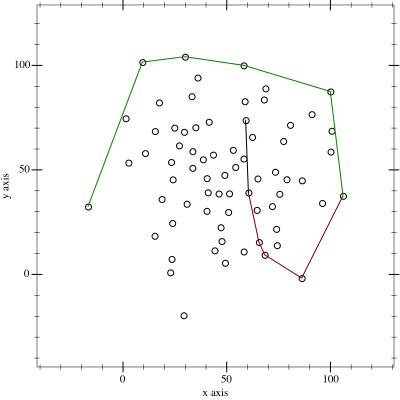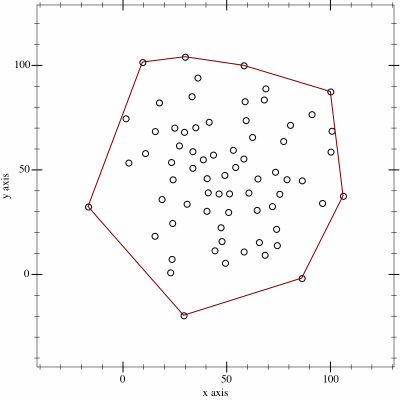
1. 전체 점들을 x축 기준, x축이 같다면 y축 기준으로 정렬한다.

2. 스택에 점들을 하나씩 넣으며, 다음 불변식을 유지하도록 삽입한다. 스택의 점들은 시계 방향으로, 즉 ccw가 음수인 방향으로 굽어 있다는 불변식을 만족해야 한다. 불변식을 만족하지 않다면 점들을 위에서부터 삭제하고 현재 점을 삽입한다.

이 과정을 통해 Upper Hull을 구할 수 있다.

3. 배열을 뒤집은 후 2의 과정을 반복한다. 이 과정을 통해 Lower Hull을 구할 수 있다.

 

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;

const int MAXN = 1e5;
const ll INF = 1e18;

struct Point
{
	ll x, y;
};

Point operator + (Point p, Point q) { return {p.x+q.x, p.y+q.y}; }
Point operator - (Point p, Point q) { return {p.x-q.x, p.y-q.y}; }

ll ccw(Point p, Point q) { return p.x*q.y-p.y*q.x; }
ll ccw(Point p, Point q1, Point q2) { return ccw(q1-p, q2-p); }

ll norm(Point p) { return p.x*p.x+p.y*p.y; }
ll dist(Point p, Point q) { return norm(p-q); }

int N;
Point A[MAXN+10];

int main()
{
	scanf("%d", &N);
	for(int i=1; i<=N; i++) scanf("%lld%lld", &A[i].x, &A[i].y);

	sort(A+1, A+N+1, [&](const Point &p, const Point &q)
	{
		if(p.x!=q.x) return p.x<q.x;
		return p.y<q.y;
	});

	vector<Point> U, D;

	for(int i=1; i<=N; i++) 
	{
		while(U.size()>1 && ccw(U[U.size()-2], U[U.size()-1], A[i])>=0) U.pop_back();
		U.push_back(A[i]);		
	}

	for(int i=N; i>=1; i--)
	{
		while(D.size()>1 && ccw(D[D.size()-2], D[D.size()-1], A[i])>=0) D.pop_back();
		D.push_back(A[i]);
	}
	printf("%d\n", U.size()+D.size()-2);
}